4. 组合逻辑1：布尔代数的规范形式及化简[英]

Combinational Logic 1: Canonical Form and Its Minimization

Logical Reasoning

Suppose the statement \(F\) is determined by two variables：
\(A\), \(B\), the relationship of \(F\) can be expressed using the logical relationship between those two varibles, for example: \(F=A.B\), then the statement is determined by the truth of \(A\),\(B\), which forms the following statement:
If \(A\) is True/False, \(B\) is True/False, Then \(F\) is True/ False.

That is Logical Reasoning.

Binary in circuits

Input and output can only have two states.
Methods of representing binary data：
- True/False - 1/0
- High/Low
- Black/White
- Level of voltage

Two ways to express binary in circuits

Positive Logic Coding（正逻辑）

• 1 is assigned to the positive or higher voltage.
  
• 0 is assigned to the negative or lower voltage.

The calculation is AND： \(F=A.B\)

Negative Logic Coding(负逻辑)

• 0 is assigned to the positive or higher voltage.
  
• 1 is assigned to the negative or lower voltage.

The calculation is OR：\(F=A+B\).

Boolean Algebra's Canonical form（布尔代数的规范化形式）

The minterm and the maxterm（最小项和最大项）

For a Boolean function of n variables:
- Minterm is a product(and) term in which each of the n variables appears once.

• Maxterm is a sum term in which each of the n variables appears once.

Minterm and maxterm are dual/inverse.

A complex system with more than one output can be considered as number of subsystems with single output and sharing common inputs.

Example: Combinational logic system 3 to 5 range indicator

3 to 5 range indicator: a system inputs 3-bit binary numbers and the output is true (1) if inputs are in the range 3 to 5. The inputs has 8 cases.
From 0 to 7 , we gets the truth table.

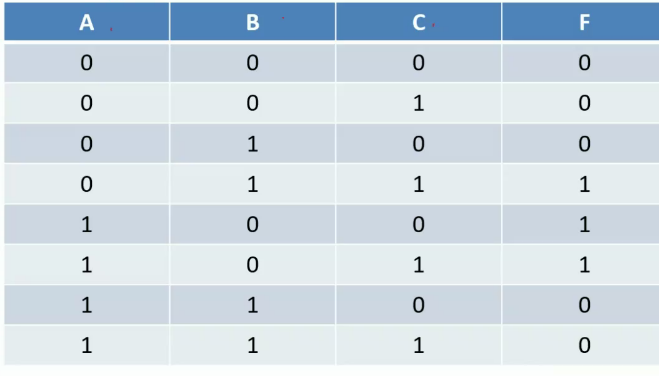
The 1st canonical form（第一范式）

In the 1st canonical form:
- Inputs are ANDed first.
- Then ORed together to get the output.

The result is minterm(最小项).

The minterm means that the conditions for inputs which satifying the output to be 1 should do the min efforts. (Only one input to be 1 is enough.)

Example: In 3 to 5 indicators, if \(F\) is 1:
The inputs of ABC are:
\[(0AND1AND1) OR (1AND0AND0) OR (1AND0AND1)\]
The description is:
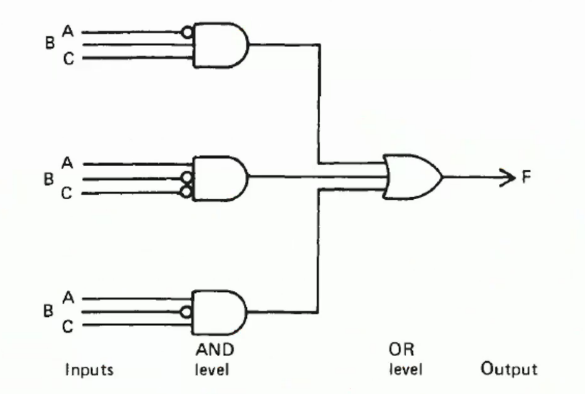
\[F=\overline{A}BC(011)+A\overline{B}\overline{C}(100)+A\overline{B}C(101)\]

This description can be drawn as a circuit:

Shorthand notation

To avoid having to write down too long Boolean equations, the T/F can be replaced by 1/0.
Example:
\[F=A'BC+AB'C'+AB'C=011+100+101\]
In decimal form, \(F=3+4+5=∑(3,4,5)\).

Example:
Transcription of \(F(ABCD)=∑(3,4,9,10)\), as 3 is 0011 4 is 0100 9 is 1001 10 is 1010.
Hence, \(F=\overline{A}\overline{B}CD+\overline{A}B\overline{C}\overline{D}+A\overline{B}\overline{C}D+A\overline{B}C\overline{D}\).

The 2nd canonical form（第二范式）

In second canonical form:
- Inputs are ORed first. - AND together to get the output

The result form is maxterm（最大项）.

The maxterm means that the conditions for inputs which satifying the output to be 1 should do the max efforts.

0 is true and 1 is not in the truth table combing the bits with OR and AND with unite.
Example: 3 to 5 indicator if F is 0.
The cases are:
000 001 010 110 111
\[\overline{F}=\overline{ABC}+\overline{A} \overline{B}C+\overline{A}B\overline{C}+AB\overline{C}+ABC\] \[F=\overline{\overline{ABC}+\overline{A} \overline{B}C+\overline{A}B\overline{C}+AB\overline{C}+ABC}\] Applying De Morgan's theorem:
\[F=(A+B+C).(A+B+\overline{C}).(A+\overline{B}+C).(\overline{A}+\overline{B}+C).(\overline{A}+\overline{B}+\overline{C})\] Or... directly use truth table

Shorthand notation

Example:
\[F=\prod(0,1,3,6,7)\]

Conversion between different canonical forms

Present each inverse number in:
- \(M\) represents the Maxterm. - \(m\) represents the Minterm. - \(I\) presents the entire logic statement (universe set, 全集).

The relationship between those are:
\[M=I - m\] Example:
in \(I=(0,1,2,3,4,5,6,7)\)
If \(M=(1,2,4,7)\), then \(m=(0,3,5,6)\),
So the 2nd canonical form is \(F=∏(1,2,4,7)\).
The 1st canonical form is \(F=∑(0,3,5,6)\).

Minimal canonical forms（最简范式）and Karnaugh map（卡诺图）

To simplify the canonical form，the minimization theorem from boolean algebra could be used on logic equation directly.
But the minimization theorem cannot guarantee the result is minimized.
The graphical method of minimizing logical functions is Karnaugh map(Kmap).
It bases on Venn Diagrams.

The coordinates of Kmap are Gray Code (In Types of Code: 2.The Gray Code(格雷码/循环码)).
Example: The Venn diagram of A AND B is:

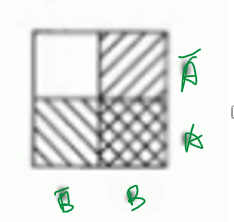
A four-celled Kmap can be obtained from replacing the shaded areas in Venn diagrams with labels on the axes.
Example: The Kmap of AND function is:

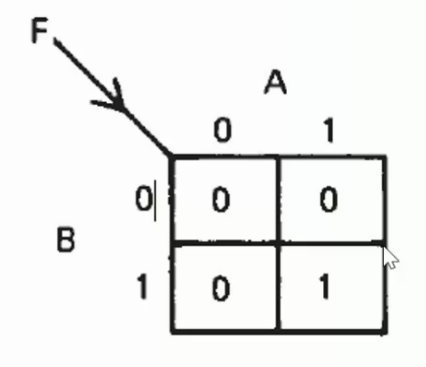
For 3 and 4 variables function functions, the Kmap is in 2 dimensions and more than 6 variables will be not adapted.

For up to 6 functions, the Kmap is in 3 dimensions.

Example: \(F=∑(0,2,4,9,11)\)
The inputs of \(F\) will be \(A B C D\)(to cover 11, 4 variables are needed).
For each minterm a 1 is placed into the Kmap All remaining cells are set to 0.

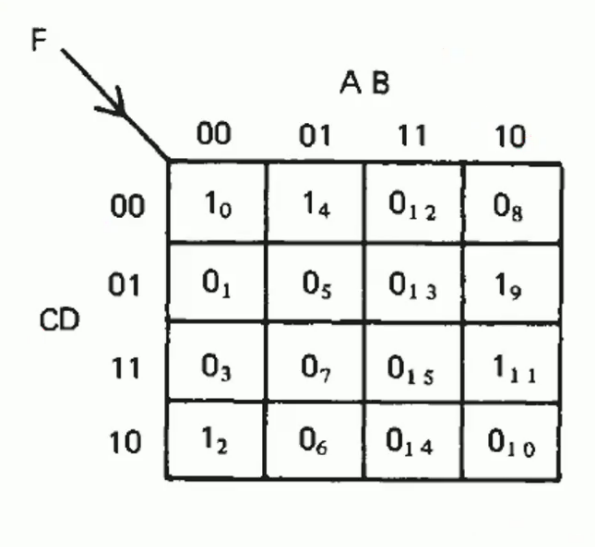
For example:
\(4=0100\)
\(A=0\) \(B=1\) \(C=0\) \(D=0\)
So the value of (01,00) is 1.

Rules of minimization

Laws of minimizing by Kmap - The numbers of effective loops(loop is not adapted to D) must be \(2^n\).
- Loops must contain \(2^n\) adjacent(相邻的) cells set to 1 or 0 for the 2nd canonical form.
A single cell cannot be simplified.
- A loop of 2 is independent of 1 variable.
- A loop of 4 is independent of 2 variables and in general a loop of \(2^n\) is independent of \(n\) variables.
- To obtain the simplest functions, the largest possible loops are used.
- All cells set to 1 must be covered when specifying the minimal form of the function.
- Loops may overlap（重叠）provided they contain at least one unlooped cell.
- Any loop that has all its cells included in other loops is redundant.（多余的）
- Loops must be square or rectangular.
- There may be different ways of looping a Kmap and the results will be different.
- The edges of Kmap are considered to be adjacent.

Example: \(F=∑(3,4,5,6,7,8,12,14)\) The variables are \(ABCD\),Kmap is:

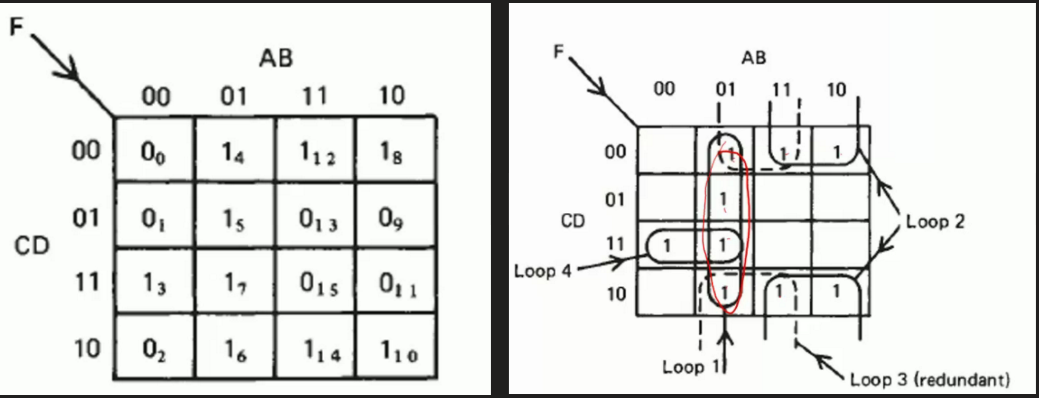
• In loop 1 values of C D have no influence on the value:
  Loop1: \(A\overline{B}\)
  
• In loop 2 value of BC have no influence on the value:
  Loop 2: \(A\overline{D}\)
• Loop 3 is a redundant loop and has no elements of itself Loop 3 is omitted.
  
• In loop 4 value of B have no influence on the value:
  Loop 4: \(\overline{A}CD\)
  \[F(ABCD)=A\overline{B}+A\overline{D}+\overline{A}CD\]

Minimization of canonical forms by using Kmap

The 1st canonical form

The minimization theorem is applicable to any minterms on the K-map that occupy adjacent cells.
- The variables that can be eliminated between a pair of minterms.
- Neighboring cells set to 1 are looped together.
- F=1 if the inputs are in loop 1 or loop 2.

Example: \(F=\overline{A}\overline{B}C+\overline{A}B\overline{C}+A\overline{B}C+AB\overline{C}\)
Kmap of \(F\) should be:

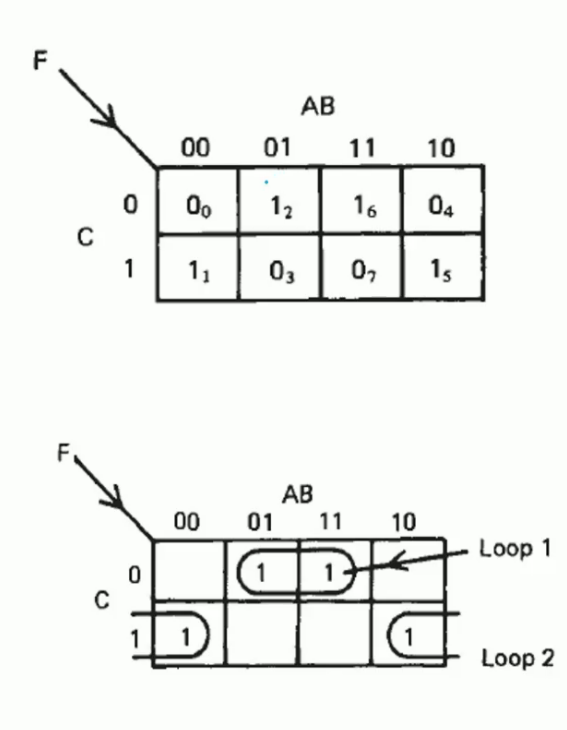
• Loop 1: B must be 1 and C must be 0; A can be 0 or 1.
  
• Loop 2: C must be 1 and B must be 0; A can be 0 or 1.
  It means that in loop 1 and loop 2, the value of A can not effect the value of F.
  So A can be removed. \[F = B\overline{C} + \overline{B}C\]

The 2nd canonical form

The minimization theorem is applicable to any maxterms on the K- map that occupy adjacent cells - The variables that can be eliminated between a pair of maxterms. - Neighboring cells set to 0 are looped together. - \(F=0\) if the inputs are in loop 1 or loop 2.

Example: \(F=(A+B+C).(A+\overline{B}+\overline{C}).(\overline{A}+B+C).(\overline{A}+\overline{B}+\overline{C})\)

• Loop 1: B must be 1 and C must be 1; A can be 0 or 1.
• Loop 2: C must be 0 and B must be 0; A can be 0 or 1. \[F=(\overline{B}+\overline{C}).(B+C)\]